Every designer, every planner,
strives to excellence. Most of the time, the standard of excellence is the
alternative with the lowest overall cost. Costs include both first costs, and
future costs. How do you compare one option to another?
This paper shows the common measures, Years-to-Payback and Cost-Performance-Index, to be invalid. Using them will lead you into gross error.
I propose, and demonstrate an alternate measure, PERFORMANCE RATIO. PERFORMANCE RATIO is easy to use, and the validity of this approach is easy to understand. First costs are added to the present value of future costs for each alternative. Present value takes into account interest and inflation rates.
PERFORMANCE RATIO may be used for simple problems using the same variables used to calculate Payback or CPI, plus interest and inflation rates.
PERFORMANCE RATIO may also be used for highly complex problems. You may break each alternative down into as many cost elements as required by the depth of your analysis. Cost elements may have different lifetimes and inflation rates. You may limit your analysis to a specific period of time. First and future cost elements are multiplied by their respective future cost multipliers.
Cost multiplier formulas are provided. Calculation of future cost multipliers becomes a simple matter of plugging in values for interest, inflation, lifetime, and analysis period. In many instances, the same multipliers may be used over a broad range of options.
The author has worked for the past 20 years at the cutting edge of innovative building technology, designing low cost, low energy building systems. The development of PERFORMANCE RATIO was a necessary consequence.
PERFORMANCE RATIO
A successful job requires a good plan. And a good plan is built on sound decisions. Most of these decisions are a tug-of-war between first cost and future performance.
Suppose you are designing a house. You are considering two different wall structures where the main difference will show up in the heat bill. You know how they differ in cost (NET COST) the construction cost difference. And, you can figure yearly fuel cost (PERFORMANCE COST) for each. How do you choose the better design?
When future performance may be measured in dollars, the decision becomes a matter of cost comparison. Unfortunately, you cannot directly compare first costs with future costs. A few attempts to deal with this have been around for a long time. Some folks like YEARS-TO-PAYBACK (YP). Others use COST-PERFORMANCE-INDEX (CPI). Many work from the seat of their pants.
THE FOLLY OF SIMPLE PAYBACK
YEARS-TO-PAYBACK
should take the cost of money and
inflation into account. Most disregard this, and use
SIMPLE-PAYBACK,
dividing
NET COST
by the yearly
PERFORMANCE COST
difference between two options.
Regardless of how you get YP, you take the shortest payback as the better
design. Think about it. A design change that has zero
NET COST,
and a tiny
PERFORMANCE COST
advantage, will deliver a top
score of zero. It will beat out another design with a small
NET COST,
but very large
PERFORMANCE COST
advantage.
YEARS-TO-PAYBACK may tell you how quickly you should recover an investment. It is not a valid measure of the better alternative!
The words COST-PERFORMANCE-INDEX might make you think CPI is the tool you need. If you have used it, you know a higher CPI means a better CPI. However, the CPI curve delivers its maximum value at zero. Check out a range of designs. As NET COST and NET PERFORMANCE go to zero, CPI goes maximum. If you use CPI, you have a built-in argument for believing your design cannot be improved.
Actually, CPI and YP are inverse relationships. If one fails, they both fail. You can not depend on YP or CPI to steer you straight. (See the description of YP and CPI in APPENDIX A).
DOING IT THE RIGHT WAY
I have worked for the past 20 years at the cutting edge of innovative building design. Low cost, low energy buildings have been the goal. Life would have been easier with a good performance test. Well, they say if you want something done right, do it yourself.
PERFORMANCE RATIO is a fairly simple idea. It compares the COSTS of two alternatives to provide a specific BENEFIT. A benefit might be work done, or the maintenance of a building's inside environment. Costs are the total of FIRST COST, and the PRESENT VALUE of all future costs.
PRESENT VALUE has a very specific meaning. It represents the current value of a future expectation. Future expectation is an estimate based on future interest and inflation rates. Suppose you make an investment today, placing $1000 in a savings account. You expect the value of that account to become considerably greater in the future. However, the PRESENT VALUE of that account is $1000.
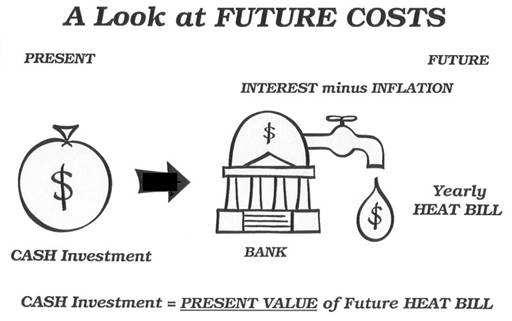
FIRST COSTS and PRESENT VALUE are equivalent. They may be summed, and compared. Let’s look at two alternatives. Providing the benefit for the first alternative represents a PRESENT VALUE of $1000. This means an investment of $1000 would produce income that precisely covers the expense of all future benefits. The second alternative costs $200 more than the first alternative. This greater FIRST COST is directly responsible for a reduction in the PRESENT VALUE cost of providing the benefit. The PRESENT VALUE of providing the benefit for the second alternative happens to be only $600. Adding this to the $200 first cost, we get $800. This is less than the $1000 required by our first alternative. Clearly, the second alternative would be our wisest investment.
PERFORMANCE RATIO makes this comparison by dividing first alternative costs by second alternative costs ($1000/$800=1.25). Division removes the effects of scale, making the result more useful for universal comparison.
When PERFORMANCE RATIO will be used to compare several alternatives, you will find it convenient to establish one of the alternatives as a BASELINE. All PR values calculated using this BASELINE may then be directly compared and ordered. Alternatives to standard practice are most easily compared using the STANDARD PRACTICE technology as the BASELINE.
My focus has been energy saving building construction. I assume the need for the benefit is perpetual. I also assume the building, with normal maintenance, will last forever. Most of you will be ready to part company with me after that last statement, but hold on for a moment. When you calculate the REPLACEMENT COST MULTIPLIER for a long lasting item like a building, you find there is almost no difference between a lifetime of 100 years and an infinite number of years.
PERFORMANCE RATIO can take both LIFETIME and benefit PERIOD into account. For those who are interested, I present the general formula for PERFORMANCE RATIO at the end of this paper. For now I shall deal with the special case using the above assumptions for PERIOD and LIFETIME.
(BASELINE COST)
(1)
PR =
───────────
(ALTERNATIVE COST)
PR > 1 alternative is BETTER
PR = 1 no change
PR < 1 alternative is WORSE
PERFORMANCE RATIO applied to the evaluation of energy conservation measures for building construction, where (NET COST) is the construction cost difference, would take the following form:
(HEAT COST)b
(2)
PR =
───────────────
(HEAT COST)a + (NET COST)a
b = BASELINE
a = ALTERNATIVE
HEAT COST (HC) is the PRESENT VALUE of the YEARLY HEAT COST (HCy). HC is equal to HCy times a COST MULTIPLIER (MC). HEAT COST is the amount of money you would have to invest such that yearly interest on the investment would equal HCy plus a reinvestment amount to offset inflation. HC is a first cost reflecting all future heating costs.
100 + F
MC =
────
(I - F)
F = AVERAGE
FUEL
INFLATION RATE
(as a PERCENT)
I
= AVERAGE
INTEREST RATE (as a PERCENT)
YEARLY HEAT COST (HCy) is equal to the sum of building ENVELOPE Conductance (U∙A) and VENTILATION Heat Loss Rate (Qv), multiplied by the number of DEGREE DAYS per year (DD), and by the ENERGY COST (EC). The FIRST-COST equivalent of total FUTURE heat cost (HC) is equal to the yearly heat cost (HCy) times the multiplier (MC) and (NC)=(NET COST).
HCy = COST/YEAR = (Uo∙Ao + Qv)∙DD∙EC
and... HC = HCy ∙ MC = (Uo∙Ao + Qv)∙DD∙EC∙MC
HCb
PR =
──────
...same as equation (2)
HCa + NCa
If the environmental factors (DD∙EC∙MC), represented by (K), are divided out, PR will appear as shown in equation (3). This is the PERFORMANCE RATIO for an entire building.
if... K = DD∙EC∙MC (K = ENVIRONMENT CONSTANT)
(Ub∙Ab + Qvb)
(3)
PR =
────────────
(building)
(Ua∙Aa + Qva) + NC/K
Notice, the value (K) represents the combined term for yearly degree days (DD), energy cost (EC), and the multiplier (MC). (K) represents all the factors over which the designer has no control, and which are site specific. A change in (K) can change the relative value of designs under consideration. Therefore, a design that is optimal in one location may not be the best design somewhere else. You should use PR for design comparison only when the PR values are calculated using the same value for (DD). (EC) and (MC) may vary only if the two designs require different fuel.
Uo = U‑VALUE of Envelope (BTU/SQ.FT./DEG.F./HOUR)
Ao = Surface AREA of Building Envelope (SQ.FT.)
Vo = VOLUME of Building Envelope (CU.FT.)
Qv = ACH∙Vo∙0.018 air change LOSS (BTU/DEG.F./HOUR)
Qv = CFM∙60∙0.018 (CFM∙60=CU.FT./HOUR, 0.018‑SHair)
DD = DEGREE DAYS (FAHRENHEIT DEGREES at location)
EC = ENERGY COST/BTU/DAY = ECbtu∙24 (24=HOURS/DAY)
APPLICATION TO BUILDING ENVELOPE SYSTEMS
It is not necessary to include terms for both envelope and ventilation heat losses when you want to examine separate building sections and components. The following example confines PR to the problem of envelope heat losses (U∙A).
In this demonstration of PR,
NET COST
is assumed to be proportional to
R‑VALUE.
Adding attic insulation would be a good example. In the real world, the difference
between competing designs does not often allow a simple relationship between
PERFORMANCE
and
NET COST.
This does not diminish the validity of PR, or its usefulness to the design process.
Moving on to real problems, let’s look at how a building's heat losses add up. The envelope sections, such as roofs and walls add together toward the total (Uo∙Ao). You may use PR to evaluate specific envelope sections (Us∙As).
So, for a given Building SECTION (s).
HCs = Us∙As∙DD∙EC∙MC
and... K=DD∙EC∙MC
so ... HCs = Us∙As∙K and... U=1/R
HCs = (1/Rs)∙(As∙K)
(1/Rb)
(4) PR =
───────────
(1/Ra) + (NC/(As∙K))
Rb = R-VALUE of baseline envelope SECTION
Ra = R-VALUE of alternative envelope SECTION
As = AREA of envelope SECTION
(As = Asb = Asa)
PERFORMANCE RATIO FOR SECTIONS OF UNIT AREA
UNIT AREA, like unit pricing, makes it easier to compare component costs. The SQUARE FOOT is the unit used in the USA. The SQUARE METER is used nearly everywhere else. By using the NET COST per UNIT AREA (COST/AREA), section AREA (As) can be removed, leaving PERFORMANCE RATIO unchanged.
NC = NET COST = (COST of B)-(COST of A)
NUIC = NET COST per UNIT AREA
(NET UNIT INCREMENTAL COST)
so ... NUIC = NC/As (and ... NC = NUIC∙As)
(1/Rb)
(5) PR =
──────────
(1/Ra) + (NUIC/K)
HEAT RECOVERY VENTILATION (HRV) SYSTEMS
PERFORMANCE RATIO also works with ventilation systems. The BASELINE used here is very simple, a standard (rather leaky) house. Equation (6) assumes the leakage rate for BASELINE is equal to the HRV rate. (This is not really fair to our HRV system, but you can make your own extrapolation.) Therefore, the difference in CFM capacity between different HRV systems does not affect PERFORMANCE RATIO. This means, you can compare any two HRV systems no matter what their CFM.
You can get into trouble comparing HRV systems. One system may run at a steady rate while another cycles on and off. Some use a defrost system that cuts in on demand, and some preheat incoming air, depending on outside temperature. Any attempt to correct for these differences will depend on installation site conditions. Affected terms are PWR, EFF, and CFM.
The assumption regarding LIFETIME, used for building construction, does not hold up for HRV systems. If you want a more accurate assessment, you may wish to replace the NET COST (NC) term with a series of incremental costs, multiplied by the appropriate REPLACEMENT COST MULTIPLIER (MR) for the respective equipment LIFETIMES. (See the general formula for PR at the end of this article.)
HC = Qv∙K
and.. HRVs use ELECTRICITY
so... K = DD∙(ECkwh∙0.007032)∙MC
NC = (HRV system COST)-(BASELINE COST)
Qv = CFM∙60∙0.018 = CFM∙1.08
(60=MINUTES/HOUR)
CFM = CFM of HRV
(Choose HRV with adequate CFH)
EFF = HRV EFFICIENCY RATING as a PERCENT
PWR = Continuous POWER RATING in WATTS
Pv = PWR∙103.8∙MONTHS(of operation)/YEAR
Equation (6) accounts for HRV POWER usage.
1
(6) PR =
───────────────────
(1-EFF/100)+(((NC/K)+(Pv/DD))/Qv)
PERFORMANCE RATIO OF AIR TIGHTNESS SYSTEMS
The following PR formulas may be used to evaluate different infiltration barrier systems. Compare nearly identical buildings, after standard depressurization testing to obtain CFM or ACH values.
Qvb
PR =
───────
Qva + (NC/K)
also... Qv = CFM∙1.08 (CFM=CUBIC FEET/MIN)
Qv = ACH∙Vo∙0.018
(ACH=AIR CHANGES/HR)
Vo = VOLUME of building
(CUBIC FEET)
K = DD∙EC∙MC
CFMb
(7a) PR =
────────────
CFMa + (NC/(1.08∙K))
ACHb
(7b) PR =
──────────────
ACHa + (NC/(Vo∙0.018∙K))
DIFFERENT ENERGY SOURCES
If different energy sources are used for the BASELINE system and ALTERNATIVE system, then you must use different (K) values for each. The value of (EC) will surely be different, and (MC) may change if the inflation rate is different for the two energy sources.
Kb = DD∙ECb∙MCb
(DD is CONSTANT)
Ka = DD∙ECa∙MCa
(Ub∙Ab + Qvb)∙Kb
(8) PR =
────────────
(Ua∙Aa + Qva)∙Ka + NC
and...
(Kb/Rb)
PR =
────────
(Ka/Ra) + NUIC
(Qvb∙Kb)
PR =
────────
(Qva∙Ka) + NC
PRACTICAL APPLICATION OF PERFORMANCE RATIO
PERFORMANCE RATIO will be more useful if you establish a BASELINE design, and compare all future designs to this baseline. I use a STANDARD PRACTICE design for my baseline. This way, I always know if a new design is better than standard practice. And, the PR value can be directly compared with PR values calculated for other designs using the same (K).
Compare PR values, including those for the same design, under different site conditions (different K values) only to assess the effect of those different conditions.
The first step to using PR is determining a value for (K). Once you have chosen (K), it does not change over the course of optimizing PR for all components, in any number of buildings using the same energy source, in a given area.
K = DD∙EC∙MC
DD = DEGREE DAYS (local FAHRENHEIT DEGREES)
EC = ECbtu∙24 = ECkwh∙0.000293∙24 = ECkwh∙0.007032
Gas or electric COST equals UTILIZATION RATE plus TAX.
CE = combustion CONVERSION EFFICIENCY (e.g. 65-95%)
MC = (100+F)/(I-F)
I = Projected AVERAGE INTEREST RATE (roughly 3 percent greater than F)
F = Projected AVERAGE FUEL INFLATION RATE
Calculating (MC) requires a careful choice of interest and inflation rates. Small differences in (I) and (F) can make a big difference in the size of (K). Luckily, PERFORMANCE RATIO is fairly insensitive to small changes in the value of (K). Use a bit of care, and take the long view. I have calculated a few sample (K) values to give you an idea of the range.
for... MC=25 and ...
A good BASELINE for comparing alternate wall structures is the standard 2x4 stud wall (1/2 inch sheetrock, vapor barrier, studs 16 inches o.c., bottom plate, double top plate, 3.5 inch fiberglass batt insulation, 3/4 inch sheathing, and 3/4 inch siding) with a composite R-VALUE (including air films) of R=12.77. It is convenient to use the standard 2x4 stud wall quoted here because (Rb) has been established, and it should be easy to cost locally.
PR = (l/Rb)/((1/Ra)+(NUIC/K))
Vary your design. Calculate the resulting PR, and choose the variation with the maximum PERFORMANCE RATIO.
REAL WORLD EXAMPLE
A study, sponsored by Energy, Mines, and Resources, CANADA used CPI to examine the relative advantage of several advanced wood frame wall designs. They were compared to a standard 2x4 stud wall. I have selected a few of the wall descriptions, in the order listed in the study report. They are presented here with the CPI given in the report, and a PR calculated using K=95 (DD=9000, EC=0.06∙(0.007), and M=25). Canadian dollars have been converted to US dollars for NUIC, but CPI values have been left as given because we only need to look at relative size and note the order.
Look at the CPI values. The wall design representing the least change has the highest CPI. As the designs move farther away, the CPI values become smaller. The study report goes on to observe that, the upgrade from a 2x4 to a 2x6 system SHOULD BE NOTED because it achieved a CPI approaching twice the CPI of the next highest wall system. This leads architects, builders, and home buyers to the wrong conclusion.
Now look at the PR values. The system of choice, in terms of money spent for value received, is wall (3). Wall (2) runs a close 2nd. You should note any value of (K) between 75 and 195 will produce the same results. Above (K=195), even the very expensive double stud wall starts looking pretty good. The range of possible wall designs is far greater than shown here, but you will not find the winners without a tool like PERFORMANCE RATIO.
PERFORMANCE RATIO - THE UNABRIDGED VERSION
The following is a more general discussion of PERFORMANCE RATIO.
I have introduced the subject in a form that may be easily and immediately applied to energy conserving home construction. The PR relationships shown in equations (2)-(8) represent a special application of PERFORMANCE RATIO. The general form of PERFORMANCE RATIO can handle situations where BENEFITS continue without end, or for a PERIOD of limited duration. Equipment in one design may have a very long LIFETIME with no need for replacement. Another design may require regular replacement of fixed LIFETIME equipment. Any logical combination of these conditions may be compared. This includes designs with considerably different lifetimes.
C = OPERATING COST (initial yearly COST)
R = EQUIPMENT COST (initial REPLACEMENT cost)
MC = Operating COST MULTIPLIER
MR = Equipment COST MULTIPLIER
Cb∙MCb + Rb∙MRb
PR =
─────────
Ca∙MCa + Ra∙MRa
C∙MC and R∙MR may be sums where COST elements have different lifetimes or inflation rates. Thus, PERFORMANCE RATIO can handle complex systems.
Σ
(cbi∙mcbi)
+
Σ
(rbj∙mrbj)
PR =
───────────────
Σ
(cak∙mcak)
+
Σ
(ral∙mral)
Sum all bi and bj elements.
Sum all ak and al elements.
I
=
INTEREST Rate (as a percentage)
F = INFLATION Rate (as a percentage)
(INFLATION may be DIFFERENT for EACH COST ITEM.)
L = LIFETIME in years
P = PERIOD in years
II = (1+I /100)L
FF = (1+F/100)L
When calculating OPERATING COST for an INFINITE PERIOD OF TIME use:
MC = (100+F)/(I-F)
MR = 1+(FF/(II-FF))
MR = 1
(for L=200 years or more)
When calculating OPERATING COST for a LIMITED PERIOD OF TIME use:
MC = ((100+F)/(I-F))∙(1-((100+F)/(100+I))P)
MR = 1 + (FF/(II-FF))∙(1-(FF/II)[(P/L)-1])
MR = 1
(for L=PERIOD)
PERFORMANCE RATIO calculations for some long-lifetime designs may be simplified when only a portion of the COST accounts for the BENEFIT. In building thermal envelope design, only the FIRST COST difference contributes to any difference in the BENEFIT. With MR=1, substitute Rb=Rb-Rb=0, and Ra=Ra-Rb=NC in the general equation for PR above. If you also say HC=HCy∙MC=C∙MC, true for thermal envelope designs, the general equation turns into equation (2).
I developed PERFORMANCE RATIO with building design in mind. However, first and future cost problems of this type are common. For instance, try comparing standard incandescent lights with the new, high efficiency fluorescents. Even choosing a new car falls into this category.
The author has developed an innovative building system, THERMAL EFFICIENCY CONSTRUCTION. R-40 wood frame walls, built using TEC, achieve PR values greater than 2.2 at K=95. He has also authored computer software making it easy to calculate building HEATLOAD, composite R-values, and of course, PERFORMANCE RATIO.
You may contact the author directly for further information at 518-359-9300, or via email at bentley@northnet.org.
APPENDIX A
COST-PERFORMANCE-INDEX (CPI) is defined by the following relationship:
Kcpi ∙ ((1/Rb) – (1/Ra)
CPI =
───────────
NUIC
and... Kcpi = DD∙EC
(Kcpi) accounts for climate and energy cost. It is a multiplier of the entire relationship. Consequently, (Kcpi) has absolutely no affect on the relative order of competing designs - a red flag for anyone considering using CPI.
Compare this to YEARS-TO-PAYBACK (YP), commonly known as SIMPLE PAYBACK:
NC
YP =
───────
(HCyb – HCya)
(HCyb – HCya) is the NET yearly HEATING COST savings for the alternate design.
For a building envelope SECTION ...
HCy = (1/R)∙A∙DD∙EC = (1/R)∙A∙Kyp
where...
Kyp = DD∙EC
(Kyp) is a common factor of both (HCyb) and (Hcya). Therefore, (Kyp) is a multiplier like (Kcpi), and with the same consequences.
and... NC = NUIC∙A so ...
NUIC
YP =
───────────
Kcpi ∙ ((1/Rb) – (1/Ra)
therefore... CPI = 1/YP
A few minor manipulations show that YP is the inverse of CPI. This means both methods will produce identical results on their inverse scales when used to judge alternative designs. YP may be useful to someone who wants to know how quickly an investment will be recovered. This information will not determine the better option.
APPENDIX B
This appendix describes the method used to derive the multipliers, (MC) and (MR). The approach is straightforward, and the math is simple. I shall start by finding the COST MULTIPLIER (MC) for an infinite PERIOD.
IF I = Interest (as a percent)
for an INCREMENT of time (say 1 year), and
F = Inflation
(as a percent)
for the same INCREMENT of time,
THEN i=(1+I/100) and f=(1+F/100)
are multipliers that may be used to calculate the new value of an
AMOUNT, after the given INCREMENT, when the amount is subject
to an increase resulting from interest, or inflation.
We want a multiplier (MC) that, when multiplied by a cost (C), will deliver an AMOUNT equal to the present value of all future costs. This AMOUNT (lets call it A), if invested at the prevalent interest rate, would produce sufficient interest to cover ALL future costs, even as those costs increase with inflation.
This means the AMOUNT (A), despite steady depletion by future costs, would not fall to ZERO until the entire PERIOD of time (infinity for this calculation) has expired.
Let us look at cumulative INCREMENTS of time. And, for the sake of argument, assume at each INCREMENT it is the final INCREMENT of the PERIOD.
Ai-Cf = 0
so.. A=C(f/i)
(Ai-Cf)i-Cf2 = 0
so.. A=C((f/i)+(f/i)2)
((Ai-Cf)i-Cf2)i-Cf3) = 0
so.. A=C((f/i)+(f/i)2+(f/i)3)
We note the series: A=C [Z+Z2+Z3+...+Zn]
and... A=C [MC] so... MC = [Z+Z2+Z3+...+Zn]
for... Z=(f/i)=(1+F/100)/(1+I/100) and... n=PERIOD
This series converges: MCn→∞ = Z/(1-Z) ...for F<I
MC = (100+F)/(I-F)
Sometimes we wish to compare alternatives where the BENEFIT PERIOD is finite. We shall now find (MC) for a finite PERIOD of time (P), a series of (P) terms.
MC = [Z+Z2+Z3+...+ZP]
and...
the original infinite series may be expressed as:
MC∞ = [Z+Z2+Z3+...+ZP]
+ ZP [Z+Z2+Z3+...+Zn]
MC∞ = MC + ZP [MC∞]
so...
MC = MC∞ (1-ZP)
MC = ((100+F)/(I-F))∙(1-((100+F)/(100+I))P)
I have derived (MC) for operating costs. These are costs (C), similar to an electric bill, where you receive a benefit and pay the bill afterward. The charges come due in roughly the same regular manner as interest payments on a bank deposit.
We shall now consider replacement costs (R), and the multiplier (MR). Replacement costs begin with initial cost (first cost). You pay in advance, and then enjoy the benefits. This is a fundamental difference between (R) and (C). Each element of this first cost has an associated LIFETIME. Elements, like planning, may be considered to have an infinite life. Hard construction elements may have such long LIFETIMES we may consider them to last forever. Many elements will require replacement at regular intervals, and some elements may have redeemable useful life at the conclusion of the BENEFIT PERIOD.
The replacement cost multiplier (MR) times the REPLACEMENT COST (R) is equal to the FIRST COST plus the PRESENT VALUE of any future replacement, based on first cost LIFETIME.
This is expressed as R∙MR where R=(REPLACEMENT COST).
MR = 1 + (future replacement PRESENT VALUE)
If LIFETIME is equal to BENEFIT PERIOD, there will never be need for replacement, or investment recovery, so for L=P :
MR = 1
For any case where LIFETIME is significantly longer or shorter than BENEFIT PERIOD, we must calculate (MR) differently.
Replacement occurs only at the end of LIFETIME. LIFETIME is measured in MULTIPLE INCREMENTS. (I) and (F) are based on SINGLE INCREMENTS. This requires definition of effective interest and inflation rates, similar to a calculation of YIELD for interest compounded at more frequent intervals.
II = ieffective =
(1+I
/100)L
FF = feffective = (1+F/100)L
ZZ = Zeffective = FF/II
We must also define an effective PERIOD (Peffective). LIFETIME becomes the effective INCREMENT. The number of replacements equals P/L less 1 because replacement is not required at the end of the BENEFIT PERIOD.
Peffective = (P/L) - 1
Using MC = (Z/(1-Z))∙(1-ZP) as a guide, substitute ZZ for Z, and Peffective for P, keeping in mind the addition of 1 to the whole thing to account for FIRST COST.
MR = 1 + (ZZ/(1-ZZ))∙(1-ZZ[(P/L)-1])
MR = 1 + (FF/(II-FF))∙(1-(FF/II)[(P/L)-1])
In the case where the PERIOD (P) goes to infinity, the relationship condenses to:
MR = 1 + (FF/(II-FF))
References
California Public Utilities Commission
California Energy Commission
Energy Efficiency and Local Assistance Division. December 1987
Don Schwartz, Project Leader.
STANDARD PRACTICE MANUAL – Economic Analysis of Demand-Side
Management Programs – Staff Report.
HD9685 .U5 E26
Proskiw, P. Eng., J. Beckman, June 1988. Incremental Costs of Energy
Conservation Systems.
Flair Homes Project REPORT NO. 2
Published by the authority of the Minister of Energy, Mines and
Resources Canada, Government of Canada.
Supplement added after Publication
LIFE CYCLE COSTING vs. PERFORMANCE RATIO
LCC is the sum of two main terms, the initial COST of the equipment being evaluated (equivalent to R∙MR where MR=1, that is PERIOD=LIFETIME), plus a future COST term consisting of yearly operating COST times LIFETIME, times a DISCOUNT FACTOR. If done right the DISCOUNT FACTOR should be equivalent to C∙MC where:
MC = [(100+F)/(I-F)]∙[1-((100+F)/(100+I))P]
where the PERIOD (P) = LIFETIME of the equipment
However, I haven’t seen enough on LCC to know whether or not the DISCOUNT FACTOR is calculated in this manner. In any case, the DISCOUNT FACTOR should be a function of the LIFETIME. LCC disguises this fact in its multiplication of LIFETIME by DISCOUNT FACTOR. It makes these terms appear to be independent variables, and this can lead to serious errors when used by those not thoroughly familiar with the derivation of the DISCOUNT FACTOR.
LCC does not lend itself to easy application to complex problems involving combinations of different LIFETIME equipment, and to PERIODS approaching infinity. It cannot be applied to comparisons involving equipment having significantly different LIFETIMES. You will face none of these problems using PERFORMANCE RATIO.
SUMMARY
PERFORMANCE RATIO is the only clear choice when you need to decide among alternatives. Required parameters are the same as used for calculating SIMPLE PAYBACK (YP) with the addition of interest rate and inflation. Over the long term, interest rate runs about 3 percent above inflation, so a rapid estimate may set (F=0) and (I=3).
PERFORMANCE RATIO is also the tool to use when making an assessment of relative environmental impact. Substitute REAL WORLD COST in place of MARKET COST. REAL WORLD COSTS would take into account future costs of depletion, remediation costs for environmental degradation including such giant issues as global warming and threats to the biosphere due to species extinction, and current and future health costs to workers and the general population.
Everyone who makes decisions with long term consequences, and that includes that ubiquitous decision to carry on as usual, should learn the value to our collective future of the importance of proper cost-benefit assessments.
PERFORMANCE RATIO - back of the envelope calculations
Historically, interest rates run about 3 percent above inflation. Put this number through the MC equation for the infinite scenario to find the future cost multiplier:
Lets round this off to an easy-to-work-with 35. This is easy to rationalize because the inflation rate for energy, especially if will be coming from an oil well, is likely to be higher than costs that derive from renewable sources so even going to 40 wouldn’t be too much of a stretch.
Multiply this MC (MC=35) by a yearly future cost. Your answer will be a good estimate for the PRESENT VALUE of that cost item. For example, suppose a house has a $2000 yearly heating bill. This means the PRESENT VALUE of that heating bill for all future time would be in the neighborhood of $70,000.
You are also considering another house, an energy efficient house that has a yearly heating bill of only $200, the PRESENT VALUE of all future heating bills for this more efficient house would be only $7000.
The difference, $63,000, would be the amount you could afford to pay extra for that energy efficient house and still break even. However, you would be greatly reducing your carbon footprint, contributing far less to global warming, and if that doesn’t warm your heart the additional comfort of an energy efficient house will most certainly do so.
If the price difference between the old technology house with that $2000 yearly heat bill and the energy efficient house is less than $63,000, you will come out ahead on all fronts with the energy efficient house.
Richard Bentley (518-359-9300) bentley@northnet.org
This paper shows the common measures, Years-to-Payback and Cost-Performance-Index, to be invalid. Using them will lead you into gross error.
I propose, and demonstrate an alternate measure, PERFORMANCE RATIO. PERFORMANCE RATIO is easy to use, and the validity of this approach is easy to understand. First costs are added to the present value of future costs for each alternative. Present value takes into account interest and inflation rates.
PERFORMANCE RATIO may be used for simple problems using the same variables used to calculate Payback or CPI, plus interest and inflation rates.
PERFORMANCE RATIO may also be used for highly complex problems. You may break each alternative down into as many cost elements as required by the depth of your analysis. Cost elements may have different lifetimes and inflation rates. You may limit your analysis to a specific period of time. First and future cost elements are multiplied by their respective future cost multipliers.
Cost multiplier formulas are provided. Calculation of future cost multipliers becomes a simple matter of plugging in values for interest, inflation, lifetime, and analysis period. In many instances, the same multipliers may be used over a broad range of options.
The author has worked for the past 20 years at the cutting edge of innovative building technology, designing low cost, low energy building systems. The development of PERFORMANCE RATIO was a necessary consequence.
PERFORMANCE RATIO
A successful job requires a good plan. And a good plan is built on sound decisions. Most of these decisions are a tug-of-war between first cost and future performance.
Suppose you are designing a house. You are considering two different wall structures where the main difference will show up in the heat bill. You know how they differ in cost (NET COST) the construction cost difference. And, you can figure yearly fuel cost (PERFORMANCE COST) for each. How do you choose the better design?
When future performance may be measured in dollars, the decision becomes a matter of cost comparison. Unfortunately, you cannot directly compare first costs with future costs. A few attempts to deal with this have been around for a long time. Some folks like YEARS-TO-PAYBACK (YP). Others use COST-PERFORMANCE-INDEX (CPI). Many work from the seat of their pants.
YEARS-TO-PAYBACK may tell you how quickly you should recover an investment. It is not a valid measure of the better alternative!
The words COST-PERFORMANCE-INDEX might make you think CPI is the tool you need. If you have used it, you know a higher CPI means a better CPI. However, the CPI curve delivers its maximum value at zero. Check out a range of designs. As NET COST and NET PERFORMANCE go to zero, CPI goes maximum. If you use CPI, you have a built-in argument for believing your design cannot be improved.
Actually, CPI and YP are inverse relationships. If one fails, they both fail. You can not depend on YP or CPI to steer you straight. (See the description of YP and CPI in APPENDIX A).
I have worked for the past 20 years at the cutting edge of innovative building design. Low cost, low energy buildings have been the goal. Life would have been easier with a good performance test. Well, they say if you want something done right, do it yourself.
PERFORMANCE RATIO is a fairly simple idea. It compares the COSTS of two alternatives to provide a specific BENEFIT. A benefit might be work done, or the maintenance of a building's inside environment. Costs are the total of FIRST COST, and the PRESENT VALUE of all future costs.
PRESENT VALUE has a very specific meaning. It represents the current value of a future expectation. Future expectation is an estimate based on future interest and inflation rates. Suppose you make an investment today, placing $1000 in a savings account. You expect the value of that account to become considerably greater in the future. However, the PRESENT VALUE of that account is $1000.

FIRST COSTS and PRESENT VALUE are equivalent. They may be summed, and compared. Let’s look at two alternatives. Providing the benefit for the first alternative represents a PRESENT VALUE of $1000. This means an investment of $1000 would produce income that precisely covers the expense of all future benefits. The second alternative costs $200 more than the first alternative. This greater FIRST COST is directly responsible for a reduction in the PRESENT VALUE cost of providing the benefit. The PRESENT VALUE of providing the benefit for the second alternative happens to be only $600. Adding this to the $200 first cost, we get $800. This is less than the $1000 required by our first alternative. Clearly, the second alternative would be our wisest investment.
PERFORMANCE RATIO makes this comparison by dividing first alternative costs by second alternative costs ($1000/$800=1.25). Division removes the effects of scale, making the result more useful for universal comparison.
When PERFORMANCE RATIO will be used to compare several alternatives, you will find it convenient to establish one of the alternatives as a BASELINE. All PR values calculated using this BASELINE may then be directly compared and ordered. Alternatives to standard practice are most easily compared using the STANDARD PRACTICE technology as the BASELINE.
My focus has been energy saving building construction. I assume the need for the benefit is perpetual. I also assume the building, with normal maintenance, will last forever. Most of you will be ready to part company with me after that last statement, but hold on for a moment. When you calculate the REPLACEMENT COST MULTIPLIER for a long lasting item like a building, you find there is almost no difference between a lifetime of 100 years and an infinite number of years.
PERFORMANCE RATIO can take both LIFETIME and benefit PERIOD into account. For those who are interested, I present the general formula for PERFORMANCE RATIO at the end of this paper. For now I shall deal with the special case using the above assumptions for PERIOD and LIFETIME.
PERFORMANCE RATIO applied to the evaluation of energy conservation measures for building construction, where (NET COST) is the construction cost difference, would take the following form:
HEAT COST (HC) is the PRESENT VALUE of the YEARLY HEAT COST (HCy). HC is equal to HCy times a COST MULTIPLIER (MC). HEAT COST is the amount of money you would have to invest such that yearly interest on the investment would equal HCy plus a reinvestment amount to offset inflation. HC is a first cost reflecting all future heating costs.
YEARLY HEAT COST (HCy) is equal to the sum of building ENVELOPE Conductance (U∙A) and VENTILATION Heat Loss Rate (Qv), multiplied by the number of DEGREE DAYS per year (DD), and by the ENERGY COST (EC). The FIRST-COST equivalent of total FUTURE heat cost (HC) is equal to the yearly heat cost (HCy) times the multiplier (MC) and (NC)=(NET COST).
and... HC = HCy ∙ MC = (Uo∙Ao + Qv)∙DD∙EC∙MC
If the environmental factors (DD∙EC∙MC), represented by (K), are divided out, PR will appear as shown in equation (3). This is the PERFORMANCE RATIO for an entire building.
if... K = DD∙EC∙MC (K = ENVIRONMENT CONSTANT)
Notice, the value (K) represents the combined term for yearly degree days (DD), energy cost (EC), and the multiplier (MC). (K) represents all the factors over which the designer has no control, and which are site specific. A change in (K) can change the relative value of designs under consideration. Therefore, a design that is optimal in one location may not be the best design somewhere else. You should use PR for design comparison only when the PR values are calculated using the same value for (DD). (EC) and (MC) may vary only if the two designs require different fuel.
Uo = U‑VALUE of Envelope (BTU/SQ.FT./DEG.F./HOUR)
Ao = Surface AREA of Building Envelope (SQ.FT.)
Vo = VOLUME of Building Envelope (CU.FT.)
Qv = ACH∙Vo∙0.018 air change LOSS (BTU/DEG.F./HOUR)
Qv = CFM∙60∙0.018 (CFM∙60=CU.FT./HOUR, 0.018‑SHair)
DD = DEGREE DAYS (FAHRENHEIT DEGREES at location)
EC = ENERGY COST/BTU/DAY = ECbtu∙24 (24=HOURS/DAY)
It is not necessary to include terms for both envelope and ventilation heat losses when you want to examine separate building sections and components. The following example confines PR to the problem of envelope heat losses (U∙A).
|
Graphic EXAMPLE (numbers used have no units, and are for example only)
HCbase K∙A = 4 (chosen for EXAMPLE) PR = ─────────────────────────── HC = K∙A/R (HEATING COST) HCalternative + NCalternate NC = Ra – Rbase (NEW COST) |
|
In the columns below, each letter R represents COST of 0.5 units of INSULATION.
Each HC represent 0.5 units of heating COST associated with the total of R above it. |
|
BASELINE ALTERNATIVES - - - - - (adding units of INSULATION) - - - - - - - >
R Rb=1 R Ra=1.5 R Ra=2 R Ra=2.5 R Ra=3 R Ra=3.5 R Ra=4 R NC=O.... R ......... R ......... R ......... R ......... R ......... R ...... HC R NC=0.5 R NC R NC R NC R NC R NC HC HC R NC=1 R NC R NC R NC R NC HC HC HC R NC=1.5 R NC R NC R NC HC HC HC HC R NC=2 R NC R NC HC HC HC HC HC R NC=2.5 R NC HC HC HC HC=2 HC HC=1.6 HC HC R NC=3 HC .. HC=2.67 .. HC=1.33 HC HC=1.14 HC HC HC=4 HC HC=1 (PR=1.33) PR=1.26 PR=1.29 PR=1.2 PR=1.1 ...PR=1 ...................................................................PR=1 |
Moving on to real problems, let’s look at how a building's heat losses add up. The envelope sections, such as roofs and walls add together toward the total (Uo∙Ao). You may use PR to evaluate specific envelope sections (Us∙As).
So, for a given Building SECTION (s).
so ... HCs = Us∙As∙K and... U=1/R
UNIT AREA, like unit pricing, makes it easier to compare component costs. The SQUARE FOOT is the unit used in the USA. The SQUARE METER is used nearly everywhere else. By using the NET COST per UNIT AREA (COST/AREA), section AREA (As) can be removed, leaving PERFORMANCE RATIO unchanged.
NC = NET COST = (COST of B)-(COST of A)
NUIC = NET COST per UNIT AREA
so ... NUIC = NC/As (and ... NC = NUIC∙As)
PERFORMANCE RATIO also works with ventilation systems. The BASELINE used here is very simple, a standard (rather leaky) house. Equation (6) assumes the leakage rate for BASELINE is equal to the HRV rate. (This is not really fair to our HRV system, but you can make your own extrapolation.) Therefore, the difference in CFM capacity between different HRV systems does not affect PERFORMANCE RATIO. This means, you can compare any two HRV systems no matter what their CFM.
You can get into trouble comparing HRV systems. One system may run at a steady rate while another cycles on and off. Some use a defrost system that cuts in on demand, and some preheat incoming air, depending on outside temperature. Any attempt to correct for these differences will depend on installation site conditions. Affected terms are PWR, EFF, and CFM.
The assumption regarding LIFETIME, used for building construction, does not hold up for HRV systems. If you want a more accurate assessment, you may wish to replace the NET COST (NC) term with a series of incremental costs, multiplied by the appropriate REPLACEMENT COST MULTIPLIER (MR) for the respective equipment LIFETIMES. (See the general formula for PR at the end of this article.)
so... K = DD∙(ECkwh∙0.007032)∙MC
Equation (6) accounts for HRV POWER usage.
The following PR formulas may be used to evaluate different infiltration barrier systems. Compare nearly identical buildings, after standard depressurization testing to obtain CFM or ACH values.
also... Qv = CFM∙1.08 (CFM=CUBIC FEET/MIN)
If different energy sources are used for the BASELINE system and ALTERNATIVE system, then you must use different (K) values for each. The value of (EC) will surely be different, and (MC) may change if the inflation rate is different for the two energy sources.
and...
PERFORMANCE RATIO will be more useful if you establish a BASELINE design, and compare all future designs to this baseline. I use a STANDARD PRACTICE design for my baseline. This way, I always know if a new design is better than standard practice. And, the PR value can be directly compared with PR values calculated for other designs using the same (K).
Compare PR values, including those for the same design, under different site conditions (different K values) only to assess the effect of those different conditions.
The first step to using PR is determining a value for (K). Once you have chosen (K), it does not change over the course of optimizing PR for all components, in any number of buildings using the same energy source, in a given area.
DD = DEGREE DAYS (local FAHRENHEIT DEGREES)
EC = ECbtu∙24 = ECkwh∙0.000293∙24 = ECkwh∙0.007032
|
EC = ECkwh∙0.007032
EC = ECoil∙0.017/CE EC = ECgas∙0.024/CE |
(ECkwh = COST/KWH
(ECoil = COST/GAL (ECgas = COST/THERM |
electricity)
fuel oil) natural gas) |
Gas or electric COST equals UTILIZATION RATE plus TAX.
CE = combustion CONVERSION EFFICIENCY (e.g. 65-95%)
MC = (100+F)/(I-F)
I = Projected AVERAGE INTEREST RATE (roughly 3 percent greater than F)
F = Projected AVERAGE FUEL INFLATION RATE
Calculating (MC) requires a careful choice of interest and inflation rates. Small differences in (I) and (F) can make a big difference in the size of (K). Luckily, PERFORMANCE RATIO is fairly insensitive to small changes in the value of (K). Use a bit of care, and take the long view. I have calculated a few sample (K) values to give you an idea of the range.
for... MC=25 and ...
|
DD=7500
DD=7500 DD=8500 DD=8500 |
EC=(0.06 ECkwh)∙(0.007032)
EC=(0.10 ECkwh)∙(0.007032) EC=(0.06 ECkwh)∙(0.007032) EC=(0.10 ECkwh)∙(0.007032) |
K=
K= K= K= |
79.1
132.9 89.7 149.4 |
A good BASELINE for comparing alternate wall structures is the standard 2x4 stud wall (1/2 inch sheetrock, vapor barrier, studs 16 inches o.c., bottom plate, double top plate, 3.5 inch fiberglass batt insulation, 3/4 inch sheathing, and 3/4 inch siding) with a composite R-VALUE (including air films) of R=12.77. It is convenient to use the standard 2x4 stud wall quoted here because (Rb) has been established, and it should be easy to cost locally.
|
Rb
Ra NUIC |
= R-VALUE of BASELINE structure (B)
= R-VALUE of ALTERNATE structure (A) = (COST(A)/SQ.FT.) - (COST(B)/SQ.FT.) |
Vary your design. Calculate the resulting PR, and choose the variation with the maximum PERFORMANCE RATIO.
A study, sponsored by Energy, Mines, and Resources, CANADA used CPI to examine the relative advantage of several advanced wood frame wall designs. They were compared to a standard 2x4 stud wall. I have selected a few of the wall descriptions, in the order listed in the study report. They are presented here with the CPI given in the report, and a PR calculated using K=95 (DD=9000, EC=0.06∙(0.007), and M=25). Canadian dollars have been converted to US dollars for NUIC, but CPI values have been left as given because we only need to look at relative size and note the order.
|
WALL DESCRIPTION
|
R-VALUE | NUIC | (CPI) | (PR) |
|
(1) (2) (3) (4) |
(2x6) 24 inch o.c. 5/8 inch fiberboard sheathing (2x6) 16 inch o.c. 1 inch Glasclad insulated sheathing with Tyvek (2x6) 16 inch o.c. 2 inch Glasclad insulated sheathing with Tyvek Double Stud Wall |
20.0 24.4 28.8 40.0 |
0.31 0.65 1.07 2.97 |
47 29 20 9 |
1.47 1.64 1.39 |
Look at the CPI values. The wall design representing the least change has the highest CPI. As the designs move farther away, the CPI values become smaller. The study report goes on to observe that, the upgrade from a 2x4 to a 2x6 system SHOULD BE NOTED because it achieved a CPI approaching twice the CPI of the next highest wall system. This leads architects, builders, and home buyers to the wrong conclusion.
Now look at the PR values. The system of choice, in terms of money spent for value received, is wall (3). Wall (2) runs a close 2nd. You should note any value of (K) between 75 and 195 will produce the same results. Above (K=195), even the very expensive double stud wall starts looking pretty good. The range of possible wall designs is far greater than shown here, but you will not find the winners without a tool like PERFORMANCE RATIO.
The following is a more general discussion of PERFORMANCE RATIO.
I have introduced the subject in a form that may be easily and immediately applied to energy conserving home construction. The PR relationships shown in equations (2)-(8) represent a special application of PERFORMANCE RATIO. The general form of PERFORMANCE RATIO can handle situations where BENEFITS continue without end, or for a PERIOD of limited duration. Equipment in one design may have a very long LIFETIME with no need for replacement. Another design may require regular replacement of fixed LIFETIME equipment. Any logical combination of these conditions may be compared. This includes designs with considerably different lifetimes.
C = OPERATING COST (initial yearly COST)
R = EQUIPMENT COST (initial REPLACEMENT cost)
MC = Operating COST MULTIPLIER
MR = Equipment COST MULTIPLIER
C∙MC and R∙MR may be sums where COST elements have different lifetimes or inflation rates. Thus, PERFORMANCE RATIO can handle complex systems.
When calculating OPERATING COST for an INFINITE PERIOD OF TIME use:
When calculating OPERATING COST for a LIMITED PERIOD OF TIME use:
PERFORMANCE RATIO calculations for some long-lifetime designs may be simplified when only a portion of the COST accounts for the BENEFIT. In building thermal envelope design, only the FIRST COST difference contributes to any difference in the BENEFIT. With MR=1, substitute Rb=Rb-Rb=0, and Ra=Ra-Rb=NC in the general equation for PR above. If you also say HC=HCy∙MC=C∙MC, true for thermal envelope designs, the general equation turns into equation (2).
I developed PERFORMANCE RATIO with building design in mind. However, first and future cost problems of this type are common. For instance, try comparing standard incandescent lights with the new, high efficiency fluorescents. Even choosing a new car falls into this category.
The author has developed an innovative building system, THERMAL EFFICIENCY CONSTRUCTION. R-40 wood frame walls, built using TEC, achieve PR values greater than 2.2 at K=95. He has also authored computer software making it easy to calculate building HEATLOAD, composite R-values, and of course, PERFORMANCE RATIO.
You may contact the author directly for further information at 518-359-9300, or via email at bentley@northnet.org.
APPENDIX A
COST-PERFORMANCE-INDEX (CPI) is defined by the following relationship:
and... Kcpi = DD∙EC
(Kcpi) accounts for climate and energy cost. It is a multiplier of the entire relationship. Consequently, (Kcpi) has absolutely no affect on the relative order of competing designs - a red flag for anyone considering using CPI.
Compare this to YEARS-TO-PAYBACK (YP), commonly known as SIMPLE PAYBACK:
(HCyb – HCya) is the NET yearly HEATING COST savings for the alternate design.
For a building envelope SECTION ...
(Kyp) is a common factor of both (HCyb) and (Hcya). Therefore, (Kyp) is a multiplier like (Kcpi), and with the same consequences.
and... NC = NUIC∙A so ...
therefore... CPI = 1/YP
A few minor manipulations show that YP is the inverse of CPI. This means both methods will produce identical results on their inverse scales when used to judge alternative designs. YP may be useful to someone who wants to know how quickly an investment will be recovered. This information will not determine the better option.
APPENDIX B
This appendix describes the method used to derive the multipliers, (MC) and (MR). The approach is straightforward, and the math is simple. I shall start by finding the COST MULTIPLIER (MC) for an infinite PERIOD.
IF I = Interest (as a percent)
THEN i=(1+I/100) and f=(1+F/100)
We want a multiplier (MC) that, when multiplied by a cost (C), will deliver an AMOUNT equal to the present value of all future costs. This AMOUNT (lets call it A), if invested at the prevalent interest rate, would produce sufficient interest to cover ALL future costs, even as those costs increase with inflation.
This means the AMOUNT (A), despite steady depletion by future costs, would not fall to ZERO until the entire PERIOD of time (infinity for this calculation) has expired.
Let us look at cumulative INCREMENTS of time. And, for the sake of argument, assume at each INCREMENT it is the final INCREMENT of the PERIOD.
We note the series: A=C [Z+Z2+Z3+...+Zn]
and... A=C [MC] so... MC = [Z+Z2+Z3+...+Zn]
for... Z=(f/i)=(1+F/100)/(1+I/100) and... n=PERIOD
This series converges: MCn→∞ = Z/(1-Z) ...for F<I
Sometimes we wish to compare alternatives where the BENEFIT PERIOD is finite. We shall now find (MC) for a finite PERIOD of time (P), a series of (P) terms.
the original infinite series may be expressed as:
I have derived (MC) for operating costs. These are costs (C), similar to an electric bill, where you receive a benefit and pay the bill afterward. The charges come due in roughly the same regular manner as interest payments on a bank deposit.
We shall now consider replacement costs (R), and the multiplier (MR). Replacement costs begin with initial cost (first cost). You pay in advance, and then enjoy the benefits. This is a fundamental difference between (R) and (C). Each element of this first cost has an associated LIFETIME. Elements, like planning, may be considered to have an infinite life. Hard construction elements may have such long LIFETIMES we may consider them to last forever. Many elements will require replacement at regular intervals, and some elements may have redeemable useful life at the conclusion of the BENEFIT PERIOD.
The replacement cost multiplier (MR) times the REPLACEMENT COST (R) is equal to the FIRST COST plus the PRESENT VALUE of any future replacement, based on first cost LIFETIME.
This is expressed as R∙MR where R=(REPLACEMENT COST).
If LIFETIME is equal to BENEFIT PERIOD, there will never be need for replacement, or investment recovery, so for L=P :
For any case where LIFETIME is significantly longer or shorter than BENEFIT PERIOD, we must calculate (MR) differently.
Replacement occurs only at the end of LIFETIME. LIFETIME is measured in MULTIPLE INCREMENTS. (I) and (F) are based on SINGLE INCREMENTS. This requires definition of effective interest and inflation rates, similar to a calculation of YIELD for interest compounded at more frequent intervals.
We must also define an effective PERIOD (Peffective). LIFETIME becomes the effective INCREMENT. The number of replacements equals P/L less 1 because replacement is not required at the end of the BENEFIT PERIOD.
Using MC = (Z/(1-Z))∙(1-ZP) as a guide, substitute ZZ for Z, and Peffective for P, keeping in mind the addition of 1 to the whole thing to account for FIRST COST.
In the case where the PERIOD (P) goes to infinity, the relationship condenses to:
References
California Public Utilities Commission
California Energy Commission
Proskiw, P. Eng., J. Beckman, June 1988. Incremental Costs of Energy
Supplement added after Publication
LCC is the sum of two main terms, the initial COST of the equipment being evaluated (equivalent to R∙MR where MR=1, that is PERIOD=LIFETIME), plus a future COST term consisting of yearly operating COST times LIFETIME, times a DISCOUNT FACTOR. If done right the DISCOUNT FACTOR should be equivalent to C∙MC where:
However, I haven’t seen enough on LCC to know whether or not the DISCOUNT FACTOR is calculated in this manner. In any case, the DISCOUNT FACTOR should be a function of the LIFETIME. LCC disguises this fact in its multiplication of LIFETIME by DISCOUNT FACTOR. It makes these terms appear to be independent variables, and this can lead to serious errors when used by those not thoroughly familiar with the derivation of the DISCOUNT FACTOR.
LCC does not lend itself to easy application to complex problems involving combinations of different LIFETIME equipment, and to PERIODS approaching infinity. It cannot be applied to comparisons involving equipment having significantly different LIFETIMES. You will face none of these problems using PERFORMANCE RATIO.
PERFORMANCE RATIO is the only clear choice when you need to decide among alternatives. Required parameters are the same as used for calculating SIMPLE PAYBACK (YP) with the addition of interest rate and inflation. Over the long term, interest rate runs about 3 percent above inflation, so a rapid estimate may set (F=0) and (I=3).
PERFORMANCE RATIO is also the tool to use when making an assessment of relative environmental impact. Substitute REAL WORLD COST in place of MARKET COST. REAL WORLD COSTS would take into account future costs of depletion, remediation costs for environmental degradation including such giant issues as global warming and threats to the biosphere due to species extinction, and current and future health costs to workers and the general population.
Everyone who makes decisions with long term consequences, and that includes that ubiquitous decision to carry on as usual, should learn the value to our collective future of the importance of proper cost-benefit assessments.
|
PERFORMANCE RATIO may be used to MAXIMIZE Performance/Cost 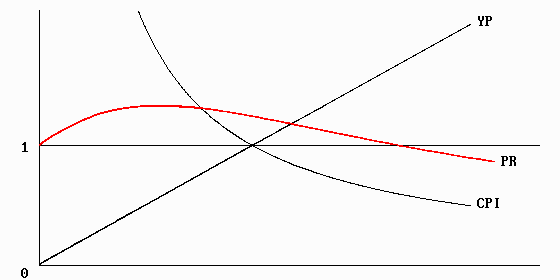 Range of ALTERNATIVES
──────>
Range of ALTERNATIVES
──────>
|
Historically, interest rates run about 3 percent above inflation. Put this number through the MC equation for the infinite scenario to find the future cost multiplier:
|
|
Lets round this off to an easy-to-work-with 35. This is easy to rationalize because the inflation rate for energy, especially if will be coming from an oil well, is likely to be higher than costs that derive from renewable sources so even going to 40 wouldn’t be too much of a stretch.
Multiply this MC (MC=35) by a yearly future cost. Your answer will be a good estimate for the PRESENT VALUE of that cost item. For example, suppose a house has a $2000 yearly heating bill. This means the PRESENT VALUE of that heating bill for all future time would be in the neighborhood of $70,000.
You are also considering another house, an energy efficient house that has a yearly heating bill of only $200, the PRESENT VALUE of all future heating bills for this more efficient house would be only $7000.
The difference, $63,000, would be the amount you could afford to pay extra for that energy efficient house and still break even. However, you would be greatly reducing your carbon footprint, contributing far less to global warming, and if that doesn’t warm your heart the additional comfort of an energy efficient house will most certainly do so.
If the price difference between the old technology house with that $2000 yearly heat bill and the energy efficient house is less than $63,000, you will come out ahead on all fronts with the energy efficient house.